If you ever want to screw over a library, just walk up to any shelf, pick up any book, and put it on another shelf where it doesn’t belong.
Eventually a librarian will stumble across it, see that it’s out of place, and pull it off the shelf. Until then, that book is hopelessly lost. It might as well be on the surface of the moon. Finding a needle in a haystack is easy. When it comes down to it, needles are not hay. Finding one book lost among a million other books? That’s hard.
The only reason such a thing as a library is possible is that it is a gigantic, life-sized, walk-in data structure, tuned for fast lookup.
This post is about searching and sorting, two fundamental aspects of data processing, and what the library has to teach us about them.
Searching
Suppose you have a sorted array,
books = [
"001.4 Graphs",
"001.56 Symbols",
...millions of strings...
"998.9 Antarctica"
]
and you want to find the position of a given value in it.
"664.75 Cookies"
How do you do that? Well, there’s a method for that:
books.index("664.75 Cookies")
But it checks every item in the array, one by one. That could take a while. Is there a better way?
Binary search is the right answer.
And this algorithm is proven optimal.
But if the sorted array looks like this

and the item you’re looking for is something like this
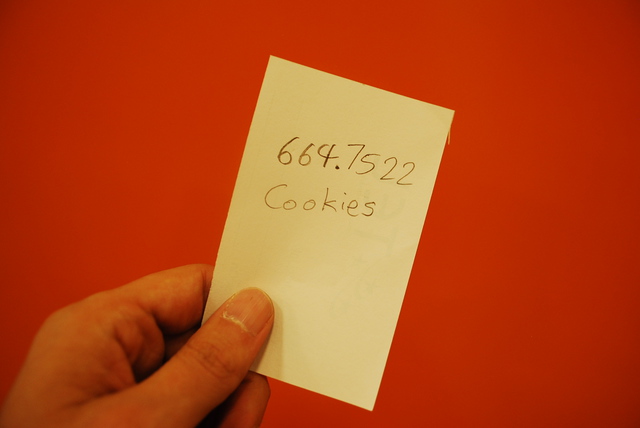
then it doesn’t feel optimal.
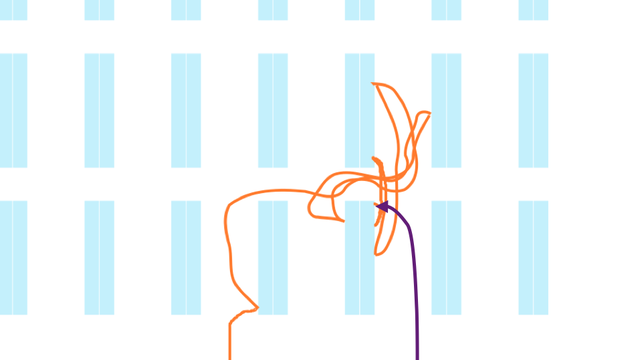
The orange path is the path you would take doing binary search. The purple path is what you want to do.
What’s going on here? Why is this optimal algorithm so bad in real life?
Is it because humans are dumb and slow and make mistakes, whereas computers are smart and fast and dependable, so what works for a computer won’t necessarily work for a human?
I don’t think so, because if I were programming a robot to go get books off the shelves, I wouldn’t have the robot do a binary search either. A robot doing binary search to find a book would look just as dumb as I would. It really is the wrong algorithm somehow.
Is it because we’re not actually searching a sorted array using comparisons? Well, no, that’s exactly what we’re doing.
So, I thought about this, and the best answer I could come up with is that the cost model is wrong.
Binary search does an optimal number of comparisons. It’s only the best algorithm if comparisons are the most significant cost.
In a library, the books are physically spread out. Most of the time it takes to find a book is not comparisons. It’s walking. And this is exactly why binary search feels so dumb: the algorithm makes no effort to minimize your walking.
There is another factor, which is that librarians do something very clever. They cheat. Or rather, they change the problem.
They put up these signs.

It’s just a little extra information. You can look at these signs and before you even start walking, you know which aisle to go to. So before you even begin, you’re already doing better than binary search.
Well, real-life programs do this exact thing in software, and for exactly the same reason.
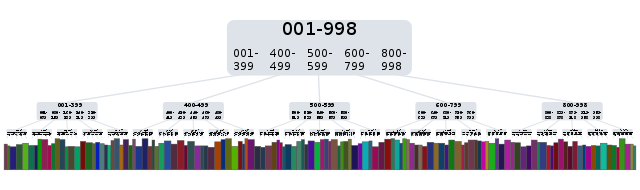
Here’s a picture of a B+ tree. Filesystems and databases basically all use this data structure or something very similar. You can see there’s a hierarchy. The actual sorted data is across the bottom; all this other stuff is just a set of signs telling what’s stored where. And all of that is a fraction of the size of the actual data. When you create an index in a database, that tree is what gets created on disk.
To find something, you start at the top, follow the signs, and in a very small number of hops, you can get to the data you’re looking for.
Now, each hop involves looking at a chunk of data and determining which way to go next. It’s some code. And if you just ignored the B+ tree and did binary search on the data itself, that would be simpler. It’d be less work, fewer CPU instructions. But it touches more pages of memory. Or disk. More walking around.
It’s easy to forget, but reading data from memory is one of the slowest things a CPU does. A modern CPU can execute hundreds of instructions in the time it takes to load anything from main memory. Going to disk is thousands of times worse.
Sorting
Everyone knows how to sort an array, right? There’s a method for that.
Unfortunately, it doesn’t work on real-world books.
>>> ().sort() TypeError
So the library must know how to sort. I mean, they’re not programmers there. But institutionally, the sorting algorithm must be there somewhere.
The standard sort methods are mostly (souped-up) merge sorts. Merge sort is O(n log n), which is optimal. So to within a small constant factor, on average, if the input is random, merge sort can’t be beat.
But if you’re sorting books, don’t use merge sort. It’s hopeless.
What the library does is a lot faster.
When books are returned to the Main library, they take them to a back room and put them on a set of shelves. There are separate shelves for popular fiction, for nonfiction, for children’s storybooks, and so on.
Every once in a while, they take all the kids’ books, put them on carts, and take them upstairs to the children’s department, where they have another set of shelves.

Same deal, only more fine-grained this time. These are the nonfiction shelves; you can’t see, but they’re labeled with Dewey Decimal numbers: 100s, 200s, and so on.
If you squint a little bit, you can see the beginning of a sorting algorithm here. Divide the data set into piles based on the first letter or first digit.
It turns out that there’s a standard name for this algorithm. It’s called bucket sort. It is in fact faster than merge sort, because—well, let’s put it this way. It’s almost exactly merge sort. But without all the annoying merging.
| merge sort | bucket sort |
|---|---|
| 1. divide (in half) | 1. divide (in bins) |
| 2. sort halves | 2. sort bins |
| 3. merge | 3. |
Instead of dividing the items arbitrarily, you’re dividing them into groups, so that when you get to the end of step 2— the 100s are sorted, the 200s are sorted, and so on— you’re done.
How is it possible for bucket sort to beat a provably optimal algorithm? Well, merge sort is as good as you can do using only comparisons. Bucket sort is cheating, because in step 1, it’s partially sorting the data without doing any comparisons at all. It can do that because the key we’re sorting on happens to be made of letters or digits. Bucket sort exploits this fact; merge sort doesn’t.
I should point out that bucket sort has pretty awful worst-case performance. You can get all the way through step 1 only to realize that all your keys started with the same letter, and so they all ended up in the same bucket, so you basically haven’t accomplished anything! This doesn’t happen to the library in practice, though.
Of course we’ve ignored the remaining problem—how do you sort the bins? And the answer is, however you want. You could bucket sort them. It could be bucket sorts all the way down.
But of course the library doesn’t do that. Because they have something even faster!
How do ordinary people sort stuff? Most of us are not terribly systematic about it, which is fine; we use a few different techniques sort of at random. But one of the main techniques that you’ll see people use again and again is what’s called insertion sort. If you’re like me, you probably learned about insertion sort in school and then promptly forgot about it because it’s O(n2). Which means it’s incredibly slow, right? Yeah, about that. Insertion sort is actually really fast. Under the right conditions.
This is a movie of me doing insertion sort on some books. I’m sorting them by color, so in the end we’ll get a nice rainbow. It’s really simple. You just put all the unsorted items in a pile on the right, and you take them one by one and put them into the output array on the left. Just insert each item in the place where it belongs so that you keep the output array sorted as you build it.
This is the fastest sorting algorithm for small arrays, up to maybe 20, 30 elements. Even in software! The only reason this sort is slow for larger arrays is that when a computer inserts an item into an array, it has to move all the other items to the right, one by one, to make room.
But you can see, inserting a book into a spot on a shelf is pretty fast. You just stick your fingers in there and slide everything over at once.
So not only is insertion sort the fastest algorithm for sorting small arrays, it’s even better suited to sorting physical books. Again, due to costs.
Pluggable algorithms
The library’s doing something kind of cool here. I never really thought about it before, but these divide-and-conquer algorithms: they’re pluggable.
The library is taking advantage of this. They use bucket sort, but not obsessively. Once they reach the point of diminishing returns, they switch over to insertion sort, which is faster for sorting small arrays.
Standard library sort routines do exactly the same thing. Most of them use merge sort, which in its purest form looks something like this:

But once they subdivide the problem down to pieces of, say, 20 items or less, they use insertion sort for those.
Some libraries go one step further, and if the array is truly unmanageably enormous, they’ll start out using quicksort, which is better for huge arrays. The problem with merge sort for big data is that it needs some temp space to work efficiently. Allocating gigabytes of memory can be bad. Quicksort can sort an array in place.
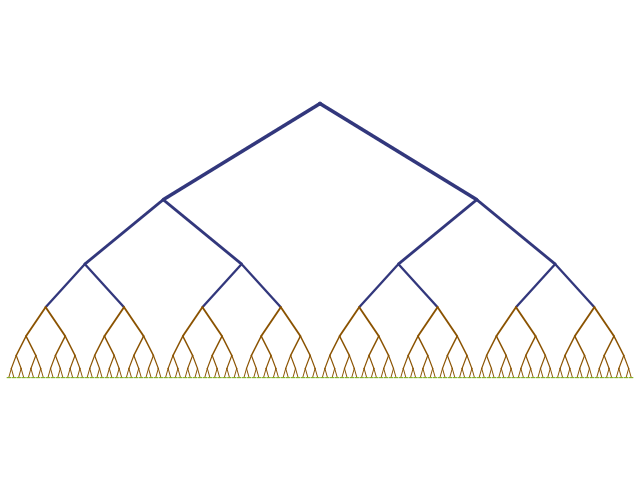
Quicksort is a divide-and-conquer algorithm too. Once it divides the data into manageable pieces, it can switch to merge sort, which will keep breaking up the data, and eventually switch to insertion sort.
Conclusion
If there’s a theme here, it is that the library is doing things that are recognizable as algorithms from computer science. But not the obvious textbook algorithms! I guess when an algorithm is going to take up a human being’s time, it tends to get optimized. These algorithms seem to be tuned very well indeed. But perhaps if you looked inside any organization you’d find something similar.
I wanted to share this because thinking about these things gave me just a slightly different perspective on programming. I just gave the library two hours a week this summer, as a volunteer, putting books on the shelves, and it turned out to be unexpectedly rewarding.
And humbling. When I started at the library, there was this moment, embarrassing now in hindsight, when I thought, hey, I know information systems. I could teach the library a thing or two! But of course, predictably, it turned out the library had something to teach me.
I don’t feel too bad about it though. Librarians have been in the IT game for a long, long time.
One more little thing. The Nashville Public Library has a great volunteer program. And they have interesting projects for web developers. They could use your talents.
Or you could just put books on the shelves. Like me. It’s about as exciting as it sounds, but I promise you this: you will read a book that you wouldn’t read otherwise.
